Problem Definition

Given: A set $Z$ of $n$ points in the plane.

Find: Smallest convex set containing $Z$.

Some Basic Definition

1. A set $S$ in the plane is convex iff for every pair of points $p_1$ and $p_2$ in $S$, the line-segment $p_1p_2 $ is in $S$.
2. A point $p$ in a convex set $S$ is said to be extreme (or a corner) iff no segment $ab$ in $S$ has $p$ in its interior.
3. $CH(Z)$ is considered to be determined once its corners ordered around the boundary are found.
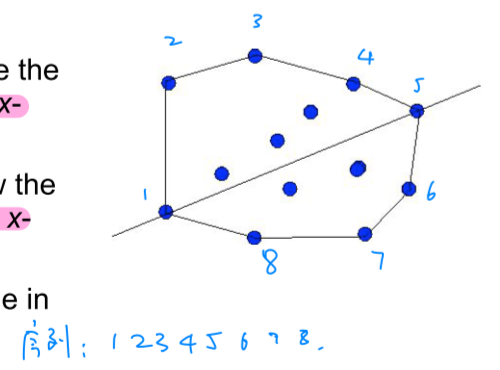
4. Simplifying assumptions: No pair of Z-points has the same x- or y-coordinate and/or no three points colinear.

Equivalent Formulations for CH

• Intersection of all convex sets containing $Z$.
• Intersection of all half-planes containing $Z$.
• Smallest possible convex set containing $Z$.
• Convex set with the smallest possible perimeter and containing $Z$.

Sorting can be transformed in $O(n)$ time into the convex hull problem. Thus the lower bound of the complexity of CH is same as sorting which is $O(n\log n)$.

Point $p_1,p_2,p_3$ make a right turn at $p_2$ iff $p_3$ is to the right or on the line through $p_1$ and $p_2$. Otherwise $p_1,p_2,p_3$ make a left turn at $p_2$. Mathematically speaking, if:

$$ det\begin{bmatrix} x_1 & y_1 & 1\\ x_2 & y_2 & 1\\ x_3 & y_3 & 1 \end{bmatrix}>0 \Rightarrow \textit{left turn} $$

Algorithm 1: Point Pruning

Since: A point in set $Z$ which is not a corner is inside a triangle on $Z$.

• Use $O(n^3)$ time to enumerate the triangles and for every triangles use $O(n)$ transverse other point to check whether it is contained. When whole procedure finishes, the remaining points never included are corners.

• Actually, we can select the left/up and right/down extreme points to form a bottom edge for triangle and enumerate the third vertex and check the other $Z$-point inclusion in $O(n\cdot n)$, cuz that the two extreme points must be included in corners.

Then, we need to sort the corners.

• Take any point in $CH(Z)$ and sort corners around it.

• Draw line through the leftmost and rightmost corners. Sort corners above the line by increasing x-coordinate and sort corners below the line by decreasing x-coordinate.

• All this can be done in $O(n\log n)$ time.

  

Algorithm 2: Edge Pruning → Jarvis March (1973)

Naïve approach:

• Arbitrarily pick one edge $O(n^2)$ and check whether all other points are located on same side of edge (left/right turn, $O(n)$ ). In total $O(n^3)$.
• Sorting of corners remains.

Jarvis’s March:

• When a boundary edge $z_iz_j$ has been identified, there must exist another boundary edge with $z_j$ as one of its endpoints.
• Boundary edge can be founded by starting from extreme point. Find boundary edge consecutively.
• Corner sorting still needed.
• $O(nh)$, where $h$ is the number of corners. Expected number of corners of points independently and uniformly distributed within a unit circle is $O(n^{1/3})$.

Algorithm 3: Graham’s Scan (1972)

Procedure:

1. Sort points around some point of CH(Z). Points at the same angle are sorted by their distance. Construct the polygon defined by the sorting.
2. Prune the nodes. If we transverse the nodes in counterclockwise (ccw) order, all middle nodes should make a left turn for pairs $p+,p,p-$, otherwise it can be removed. After remove the middle point $p$, $p-$ would go backward, otherwise all three points walk forward.
3. Algorithm terminate when the initial corner arrived by a forward step.

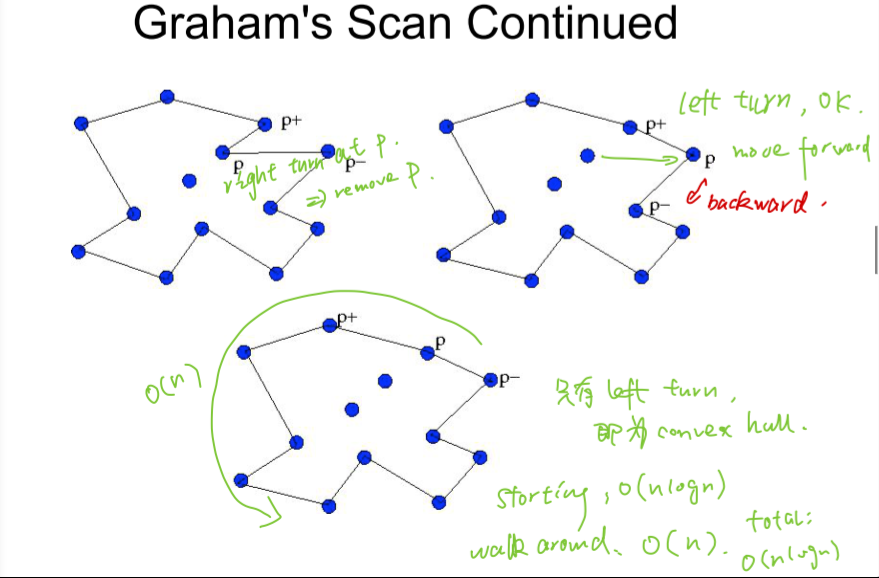
Something may goes wrong:

• Will never go backwards behind the initial corner, which means if we select a wrong initial corner at first, it would be dropped and we will never trace back to it.

Complexity:

• # of backward steps is $O(n)$.
• # of forward step is $O(n)$.
• Sorting $O(n\log n)$.
• Totally, $O(n\log n)$.

Algorithm 4: Divide and Conquer

Partition $Z$ into balanced subsets $Z_1$ and $Z_2$, determine $CH(Z_1)$ and $CH(Z_2)$ recursively. The problem solve directly if $n\leq 2$.

Merge:

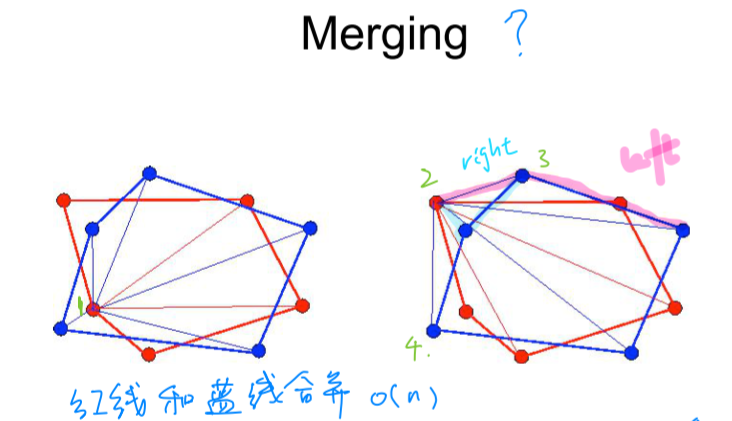
• For each merge phase, two sub-polygon with corners sorted are available. Then select one point arbitrarily, say point 1. Build two sorted edge set between point 1 and other points.
• If point 1 is inside another polygon, cause this two edges are all sorted, we can merge them directly.
• If point 2 is outside another polygon, we pick two extreme points (which is exterior most to point 2), say point 3 and point 4. For all other points $q$, we check whether it make a left turn from point 3 to point 2, or form a right turn from point 4 to point 2. If not, we drop this point. (or we can check whether this point is included by the other polygon)

Partition and union complexity:

$$ \begin{array}{c} T(n)=O(1), n \leq 2 \\ T(n)=2 * T(n / 2)+O(n), n>2 \end{array} $$

Overall $O(n\log n)$.

Algorithm 5: Marriage-before-Conquest (1986)

“Reverse Order” than Divide-and-Conquer.

Calculate the Upper and Lower Convex Hulls separately and merge them.

1. Divide the nodes into 2 points, which is approximately same.
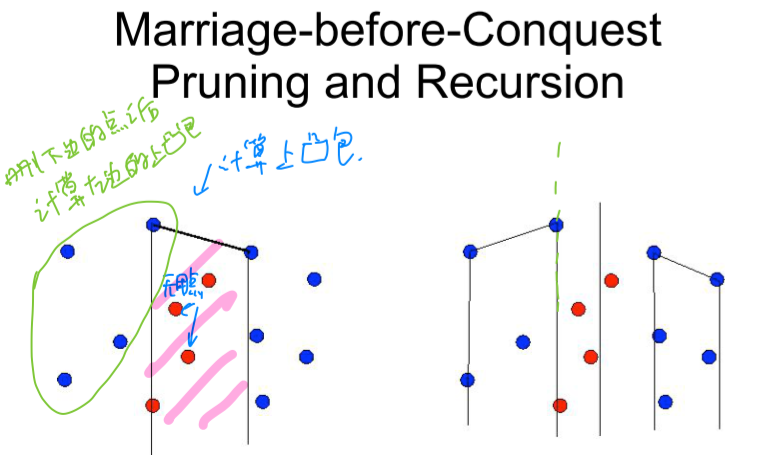
2. Find the Bridge across two sides.
3. Drop the nodes exactly below the bridge and compute the left upper CH and right upper CH recursively.
4. Merge.

How to find a Bridge?

1. Build edges by pairing two nodes arbitrarily. Select the edge $e$ with median slope.
2. Move $e$ parallelly to the upper/lower extreme point $p$ (no more higher /lower nodes exists). If exactly two nodes from both sides located in same line, the line is bridge and then be returned.
3. Otherwise, for all of other points $p_i$ in same side of $p$, calculate the slope $e_i=(p,p_i)$ . If $p$ is on left side and $e_i>e$, drop $p_i$, or if $p$ is on right side and $e_i<e$, drop $p_i$.
4. Repeat until only 1 node in opposite side of $p$ exists.

Complexity containing both Bridge Finding, and Overall Complexity is shown as follows, big constant.

Algorithm 6: Chan’s

Algorithms with complexity measured as a function of both $n$ and output size $h$ are said to be output-sensitive.

Let $P\subset E^2$ be a set of $n\geq 3$ points. The procedure of Chan’s algorithm is:

Algorithm Hull2D($P, m, H$), where $P \subset E^2$, $3 ≤ m ≤ n$, and $H ≥ 1$

1. partition $P$ into subsets $P_1,\cdots,P_{\lceil n/m\rceil}$ each of size at most $m$
2. for $i=1,\cdots, \lceil n/m\rceil$ do
   1. compute conv($P_i$) by Graham’s scan and store its vertices in an array in ccw order
3. $p_0\leftarrow (0,-\infty)$
4. $p_1\leftarrow$ the rightmost point of $P$
5. for $k=1,\cdots,H$ do
   1. for $i=1,\cdots,\lceil n/m\rceil$ do
      1. compute the points $q_i\in P_i$ that maximizes $\angle p_{k-1}p_kq_i\quad (q_i\neq p_k)$ by performing a binary search on the vertices of conv($P_i$)
   2. $p_{k+1}\rightarrow$ the point $q$ from ${q_1,\cdots,q_{\lceil n/m\rceil}}$ that maximizes $\angle p_{k-1}p_kq$
   3. if $p_{k+1}=p_1$ then return the list $\langle p_1,\cdots,p_k\rangle$
6. return incomplete

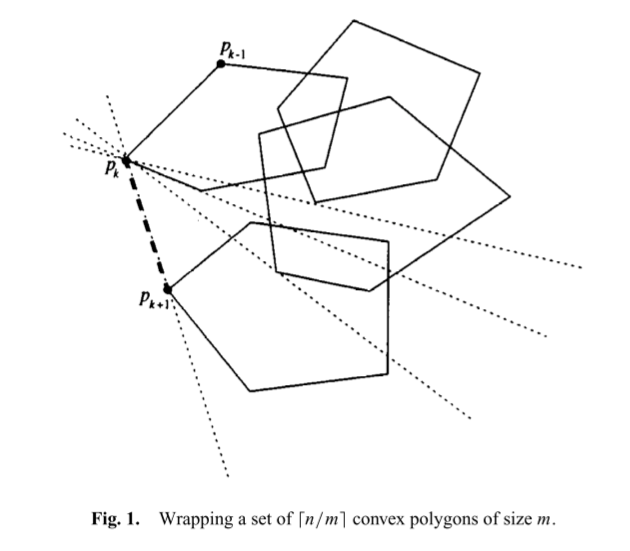
By choosing $m = H$, the complexity of the algorithm is then $O(n(1+H/m) \log m) = O(n \log H)$. Since the value of $h$ is not known in advance, we use a sequence of $H$’s to “guess” its value as shown below:

Algorithm Hull2D($P$), where $P \subset E^2$

1. for $t = 1, 2,\cdots $ do
   1. $L\rightarrow $ Hull2D($P,m,H$), where $m=H=\min{2^{2^t},n}$
   2. if $L\neq incomplete$ then return $L$

The procedure stops with the list of hull vertices as soon as the value of $H$ in the for-loop reaches or exceeds $h$. The number of iterations in the loop is $\lceil \log \log h\rceil$ (using base-2 logarithms), and the $t$-th iteration takes $O(n \log H) = O(n2^t )$ time. Therefore, the total running time of the algorithm is $O(\sum_{t=1}^{\lceil \log\log h\rceil}n2^t)=O(n2^{\lceil\log\log h\rceil+1})=O(n\log h)$. The storage requirement is clearly linear.

Reference:

• Convex Hull, CG - Lecture, UCPH-DIKU.
• Chan’s paper

Thomas Men

$\int_{birth}^{death}\text{study} dt = \text{life}$