Art gallery problem

Two points in a simple polygon can see each other if their connecting line segment is in the polygon.

Definition The art gallery problem:

​ How many points are needed in a simple polygon with $n$ vertices so that every point in the polygon is seen?

This problem is NP-hard.

Theorem art gallery theorem:

​ $\lfloor n/3\rfloor$ cameras are occasionally necessary but always sufficient.

Some Definition

• Polygon $P$ is triangulated: a decomposition of $P$ into disjoint triangles by a maximal set of non-intersecting diagonals.
• Diagonal of $P$: open line segment that connects two vertices of $P$ and fully lies in the interior of $P$.
• Dual graph for a plane graph $G$ is a graph which is, each face in primal graph gives a node; two nodes are connected in dual graph if the faces are adjacent. The dual graph of a triangulated simple polygon without hole is a tree.
• A simple polygon is y-monotone iff any horizontal line intersects it in a connected set (or not at all), or equivalently, if every horizontal line intersects it at most twice.

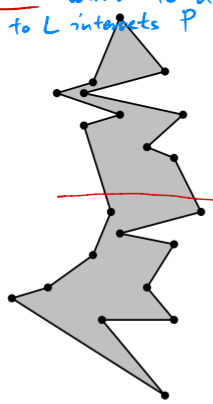
Lemma: A simple polygon with $n$ vertices can always be triangulated, and always into $n-2$ triangles.

Proof Every tree has a leaf, in particular the one that is the dual graph. Remove the corresponding triangle from the triangulated polygon, colour its vertices, add the triangle back, and let the extra vertex have the colour different from its neighbours.

For a 3-coloured, triangulated simple, one of the color classes is used by at most $\lfloor n/3\rfloor$ colors. Place the cameras at these vertices.

Triangulate a polygon

Overview:

1. Use plane sweep to partition the polygon into $y$-monotone polygons.
2. Triangulate each $y$-monotone polygon.

Partition into monotone pieces

Vertex type:

• Start, above space of the vertex does not belongs to the polygon,
• Stop/End, below space of the vertex does not belongs to the polygon,
• Split, the polygon separate into two parts after this point,
• Merge, the polygon merge into one part after this point,
• Regular.

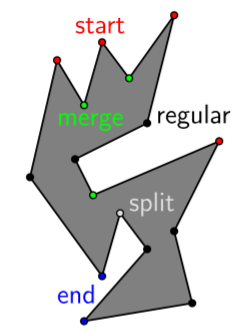
The sweep idea is, find diagonals from each merge vertex down, and from each split vertex up. Since these two kinds of points change the monotone of the polygon.

Definition The helper for an edge $e$ that has the polygon right of it, and a position of the sweep line, is the lowest vertex $v$ above the sweep line such that the horizontal line segment connecting $e$ and $v$ is inside the polygon.

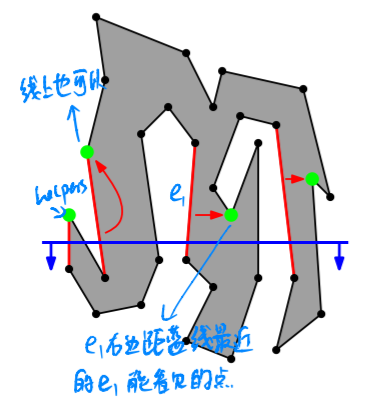
Definition The status is the set of edges intersecting the sweep line that have the polygon to their right, sorted from left to right, and each with their helper: the last vertex passed in that component. The status structure stores all edges that have the polygon to the right, with their helper, sorted from left to right in the leaves of a balanced binary search tree $T$.

The event happen only at the vertices: sort them by $y$-coordinate and put them in a list.

Now we begin sweep the initial polygon and prepare to handle the different event when the sweep line meets the vertex of:

• Start vertex $v$: insert the ccw incident edge in $T$ with $v$ as the helper (the left edge behind $v$).
• End vertex $v$: delete the clockwise incident edge and its helper from $T$ (the left edge above $v$).
• Regular vertex $v$: if the polygon is right of the two incident edges, then replace the upper edge by the lower edge in $T$, and make $v$ the helper. If the polygon is left of the two incident edges, then find the edge $e$ directly left of $v$, and replace its helper by $v$.

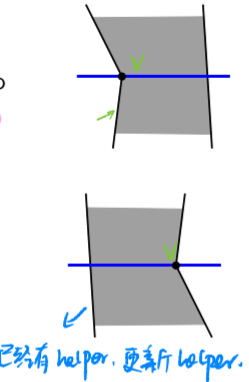
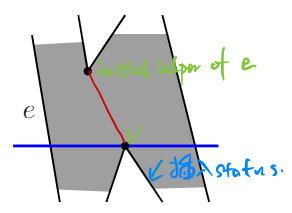
• Merge vertex $v$: Remove the edge clockwise from $v$ from $T$. Find the edge $e$ directly left of $v$, and replace its helper by $v$.

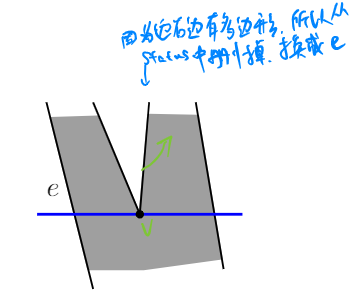
• Split vertex $v$: Find the edge $e$ directly left of $v$, and choose as a diagonal the edge between its helper and $v$. Replace the helper of $e$ by $v$. Insert the edge ccw from $v$ in $T$, with $v$ as its helper.

Efficiency:

​ Sorting all events by $y$-coordinate takes $O(n\log n)$ time. Every event takes $O(\log n)$ time, because it only involves querying, inserting and deleting in $T$.

Two-direction Sweep:

​ We need to sweep in both upward and downward direction, since unidirectional sweep is insufficient divide the polygon into monotone spices.

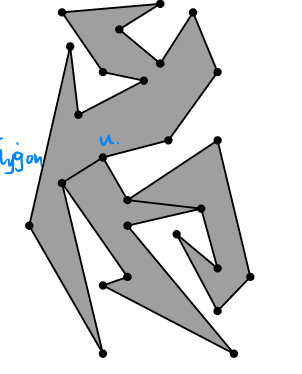
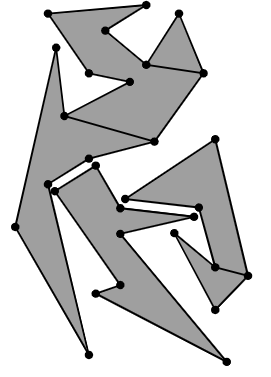
For a same vertex, maximum 2 diagonals would be chosen to the same vertex. Because, if $u$ is a split vertex, an edge is added to $u$ and the helper of $u$; then the sweep continuous, another split vertex below which regards $u$ as its helper would also add one edge to $u$, then $u$ would never become helper.

Theorem: A simple polygon with $n$ vertices can be partitioned into $y$-monotone pieces in $O(n\log n)$ time.

Triangulating a monotone polygon

The algorithm:

1. Sort the vertices top-to-bottom by a merge of the two chains,
2. Initialize a stack. Push the first two vertices,
3. Take the next vertex $v$, and triangulate as much as possible, top-down, while popping the stack,
4. Push $v$ onto the stack.

Theorem A monotone polygon with $n$ vertices can be triangulated $O(n)$ time.

Triangulating a simple polygon

We need to argue that all $y$-monotone polygons together that we will triangulate have $O(n)$ vertices.

• Initially we had $n$ edges. We add at most $n-3$ diagonals in the sweeps. These diagonals are used on both sides as edges. So all monotone polygons together have at most $n+2(n-3)=3n-6$ edges, and therefore at most $3n-6$ vertices.
• Note that the complexity all about the total computation load, hence we can conclude that triangulating all monotone polygons together takes only $O(n)$ time.

Theorem A simple polygon with $n$ vertices can be triangulated $O(n\log n)$ time.

Reference:

• Polygon Triangulation, CG - Lecture, UCPH-DIKU.
• Chan’s paper

Thomas Men

$\int_{birth}^{death}\text{study} dt = \text{life}$